Redes Neurais Artificiais Feedforward
Material produzido para disciplina de Redes Neurais Artificiais do curso de Engenharia de Computação e Software da Universidade Federal Rural do Semi-Árido (UFERSA). Professora: Rosana C. Rego.
As Redes Neurais Artificiais (RNAs) são modelos computacionais inspirados na estrutura e no funcionamento do cérebro humano. Elas têm sido amplamente utilizadas em tarefas de aprendizado supervisionado e não supervisionado, como classificação, regressão, reconhecimento de padrões e previsão de séries temporais. Seu poder vem da capacidade de aproximar funções não lineares complexas por meio de um conjunto de unidades computacionais interconectadas chamadas neurônios artificiais.
Neste capítulo, será apresentada a fundamentação teórica das RNAs, com foco nas redes do tipo feedforward, conhecidas como perceptrons e perceptrons multicamadas (MLPs). Inicialmente, abordamos o modelo matemático do neurônio artificial, seguido pela construção da rede perceptron e suas limitações. Em seguida, é discutido o clássico problema XOR, que evidencia a necessidade de arquiteturas mais profundas. Na sequência, são introduzidas as redes multicamadas, o método do gradiente para otimização de pesos, e o algoritmo de retropropagação (backpropagation), que permite a atualização eficiente dos parâmetros. Também são exploradas as principais funções de ativação e exemplos práticos de classificação e regressão utilizando RNAs.
Modelo matemático do neurônio
O cérebro humano é constituído por uma vasta e complexa rede neural formada por bilhões de neurônios interconectados. Essas células especializadas são responsáveis pela recepção, processamento e transmissão de sinais elétricos e químicos, possibilitando a comunicação entre diferentes regiões cerebrais. Cada neurônio funciona como uma unidade básica do sistema nervoso, capaz de transmitir impulsos nervosos que sustentam funções cognitivas, sensoriais e motoras.
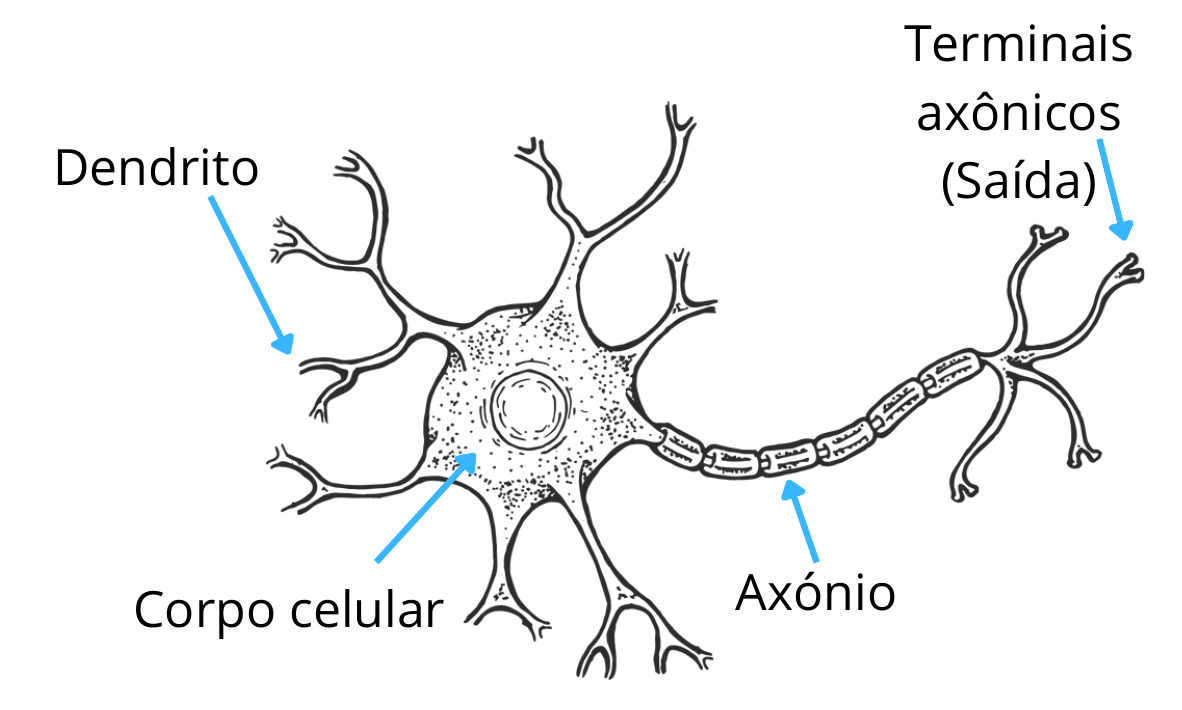
O neurônio biológico é responsável por receber, processar e transmitir informações por meio de sinais elétricos e químicos. Os sinais recebidos pelos dendritos são somados no corpo celular. Se essa soma ultrapassa um certo limite (limiar), o neurônio dispara um potencial de ação que é propagado pelo axônio para os neurônios seguintes. Conforme mostrado na Figura 1, os dendritos recebem os sinais elétricos (estímulos) de outros neurônios. O corpo celular (soma) integra os sinais recebidos e decide se um impulso será enviado adiante. Já o axônio transmite o impulso elétrico para outros neurônios ou células. E por fim, os terminais axônicos fazem a conexão com outros neurônios por meio de sinapses.
O neurônio artificial é inspirado no neurônio biológico, ele realiza uma operação matemática simples: recebe múltiplas entradas que representam os dendritos, aplica um peso a cada uma delas, soma os resultados e então aplica uma função de ativação à soma ponderada, como mostrado na Figura 2. Os pesos aplicadas a cada uma das entradas simulam a força ou influência de cada sinal recebido, já a soma ponderada representa a soma no corpo celular. O limiar de disparo é representado pelo viés e pela função de ativação, e o potencial de ação (impulso elétrico) é análogo à saída da função de ativação.
Matematicamente, o funcionamento de um neurônio pode ser descrito pela seguinte equação:
em que $x_i$ representa a entrada $i$-ésima do neurônio, $w_i$ é o peso sináptico associado à entrada $x_i$, $b$ é o viés (bias), um termo adicionado à soma ponderada para ajustar o resultado da função de ativação, $\phi(\cdot)$ é a função de ativação, responsável por introduzir não linearidades no modelo e $y$ é a saída do neurônio. Este modelo foi proposto por McCulloch e Pitts em 1943.
Como base no modelo (2), em 1958, Rosemblat apresentou uma rede neural constituída por um único neurônio chamada Rede Perceptron.
Rede Perceptron
O Perceptron, ilustrado na Figura 3, é a forma mais simples de rede neural artificial, proposta por Frank Rosenblatt em 1958. Ele foi projetado para realizar classificação binária de padrões lineares. Considere um vetor de entradas $\mathbf{x} = [x_1, x_2, ..., x_n]^T$ e um vetor de pesos $\mathbf{w} = [w_1, w_2, ..., w_n]^T$, o Perceptron calcula uma soma ponderada:
A saída do perceptron é então dada por uma função de ativação, tipicamente a função degrau de Heaviside:
Hiperplano de Decisão
Matematicamente, a equação (3) representa uma função afim que define um hiperplano no espaço $\mathbb{R}^n$. No contexto das redes neurais, especialmente no modelo do perceptron, essa expressão é utilizada para calcular a combinação linear dos valores de entrada ponderados por seus respectivos pesos, acrescida de um termo de viés. O hiperplano definido por essa equação, mais precisamente, pela condição $\mathbf{w}^T \mathbf{x} + b = 0$, funciona como uma superfície de decisão que separa o espaço de entrada em duas regiões distintas.
Conforme mostrado na Figura 4, cada lado do hiperplano corresponde a uma classe diferente: se o resultado da equação for maior ou igual a zero, isto é, classe $C_1$, o perceptron ativa (saída igual a 1); caso contrário, permanece inativo (saída igual a 0), classe $C_2$. O vetor de pesos $\mathbf{w}$ determina a orientação do hiperplano, atuando como vetor normal, enquanto o viés $b$ ajusta sua posição no espaço. Dessa forma, o perceptron realiza uma classificação linear, e a equação que o rege tem papel central na definição das fronteiras de decisão no espaço de atributos.
Exemplo: Operação OR
Vamos exemplificar o Perceptron para a função lógica OR. Isto é, desejamos que o perceptron aprenda a função OR, que tem duas entradas binárias ($x_1$ e $x_2$) e uma saída binária ($y$). A função OR retorna 1 se pelo menos uma das entradas for 1, caso contrário retorna 0. A tabela verdade da função OR é dada por:
| $x_1$ | $x_2$ | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Tabela verdade da função OR
O perceptron calcula uma combinação linear das entradas e passa por uma função de ativação degrau:
Para a função OR, uma escolha simples de pesos e bias é:
Vamos calcular o valor de $u = w_1 x_1 + w_2 x_2 + b$ e a saída do perceptron $y = f(u)$ para cada linha da tabela verdade:
| $x_1$ | $x_2$ | $u = w_1 x_1 + w_2 x_2 + b$ | Ativação $f(u)$ | Saída esperada |
|---|---|---|---|---|
| 0 | 0 | $1 \cdot 0 + 1 \cdot 0 - 0.5 = -0.5$ | 0 | 0 |
| 0 | 1 | $1 \cdot 0 + 1 \cdot 1 - 0.5 = 0.5$ | 1 | 1 |
| 1 | 0 | $1 \cdot 1 + 1 \cdot 0 - 0.5 = 0.5$ | 1 | 1 |
| 1 | 1 | $1 \cdot 1 + 1 \cdot 1 - 0.5 = 1.5$ | 1 | 1 |
Cálculos para o perceptron implementando a função OR
Observamos que o perceptron classifica corretamente todas as entradas da função OR. Graficamente, temos o seguinte hiperplano que separa as classes:
O perceptron é capaz de aprender apenas funções que podem ser separadas por uma linha (ou hiperplano em dimensões maiores). Isso significa que ele só funciona para problemas em que é possível traçar uma fronteira linear que separe as classes. Funções que exigem decisões mais complexas, como XOR, ou dados com classes que se misturam de forma não linear, não podem ser corretamente classificadas pelo perceptron simples.
Problema XOR
Um dos principais problemas que demonstra as limitações do perceptron simples é o problema XOR (ou exclusivo). A função XOR é definida por uma tabela verdade onde a saída é 1 apenas quando as entradas são diferentes:
| $x_1$ | $x_2$ | XOR($x_1$, $x_2$) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Conforme mostrado na Figura 5, a função XOR não é linearmente separável, ou seja, não existe uma linha (no caso bidimensional), um hiperplano (em dimensões maiores), que possa separar perfeitamente as classes da saída com base nas entradas. Isso significa que um perceptron simples não é capaz de resolver o problema de classificação da função XOR.
Essa limitação foi demonstrada no final da década de 1960 por Minsky e Papert, o que levou a um período de estagnação nas pesquisas com redes neurais. No entanto, a introdução das redes multicamadas (Multi-Layer Perceptrons - MLP) e o desenvolvimento do algoritmo de retropropagação (backpropagation) permitiram que redes com pelo menos uma camada oculta fossem capazes de aprender funções não linearmente separáveis, como o XOR.
Com uma arquitetura de rede composta por uma camada oculta com neurônios não lineares e uma camada de saída, é possível representar corretamente a função XOR. Isso evidenciou o poder das redes neurais multicamadas em aproximar funções arbitrárias, contribuindo para a consolidação das RNAs como uma poderosa ferramenta de aprendizado de máquina.
A Figura 5 ilustra visualmente o problema XOR no espaço bidimensional, mostrando como os pontos estão distribuídos de forma que nenhuma linha reta pode separá-los corretamente:
Redes Perceptron de Múltiplas Camadas
As redes Perceptron de Múltiplas Camadas, conhecidas como Multi-Layer Perceptrons (MLPs), são um tipo de rede neural artificial composta por, no mínimo, três camadas de neurônios: uma camada de entrada, uma ou mais camadas ocultas e uma camada de saída, conforme mostra a Figura 6. Ao contrário dos perceptrons simples, que são limitados a problemas linearmente separáveis, as MLPs são capazes de modelar relações não lineares complexas entre as entradas e as saídas.
Cada neurônio nas camadas ocultas aplica uma transformação não linear à combinação ponderada das entradas que recebe, por meio de funções de ativação como ReLU, sigmoide ou tangente hiperbólica. A presença dessas funções de ativação não lineares nas camadas ocultas permite que a rede como um todo aprenda representações complexas dos dados, aproximando funções arbitrárias com precisão suficiente. Essa propriedade é formalizada no Teorema da Aproximação Universal, que afirma que uma MLP com ao menos uma camada oculta contendo um número suficiente de neurônios pode aproximar qualquer função contínua definida em um subconjunto compacto de $\mathbb{R}^n$.
Formulação Matemática
Seja a entrada da rede dada por:
em que $n_0$ é o número de neurônios da camada de entrada. Para cada camada $l = 1, 2, \ldots, L$ e para cada neurônio $i = 1, 2, \ldots, n_l$, calculamos:
onde $w_{ij}^{(l)}$ é o peso da conexão entre o neurônio $j$ da camada $(l-1)$ e o neurônio $i$ da camada $l$, $b_i^{(l)}$ é o bias do neurônio $i$ na camada $l$, $\varphi^{(l)}$ é a função de ativação da camada $l$, e $a_i^{(l)}$ é a ativação do neurônio $i$ na camada $l$. A saída da rede é dada por:
Solução do problema XOR
Conforme discutido, o problema XOR não pode ser resolvido com um único perceptron, pois não é linearmente separável. No entanto, uma rede neural com uma única camada oculta é capaz de resolver este problema. A arquitetura mínima necessária para resolver o XOR é apresentada na Figura 7.
A rede possui uma camada de entrada com dois neurônios, correspondentes às variáveis $x_1$ e $x_2$. Uma camada oculta com dois neurônios, com função de ativação não linear, e uma camada de saída com um único neurônio, também com função de ativação não linear. A ideia principal é que os neurônios da camada oculta aprendem a representar combinações intermediárias das entradas, criando regiões no espaço que tornam o problema separável. Em seguida, o neurônio da camada de saída combina essas regiões para produzir a saída correta.
Essa estrutura transforma o problema XOR em um conjunto de duas separações lineares intermediárias, que são posteriormente combinadas de forma não linear para representar a saída desejada, conforme é mostrado na Figura 8.
Cálculo Matemático da Solução XOR
Considerando a rede com duas entradas $x_1, x_2$, dois neurônios na camada oculta ($h_1, h_2$) e um neurônio de saída $y$, utilizamos a função de ativação degrau:
As camadas ocultas são dadas pelas expressões:
E a camada de saída:
Considere os pesos da primeira camada:
E os pesos para a camada de saída:
Portanto, a tabela de cálculos para cada entrada é:
| $x_1$ | $x_2$ | $h_1$ | $h_2$ | $y$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Resultado da MLP para a função XOR
Você pode estar se perguntando: como encontrar os melhores pesos? Os pesos de uma rede neural são calculados automaticamente durante o processo de treinamento. No processo de treinamento das MLPs o algoritmo de retropropagação (backpropagation) ajusta os pesos e vieses da rede utilizando técnicas de otimização como o gradiente descendente. Durante o treinamento, o erro entre a saída da rede e o valor desejado é propagado de volta pelas camadas, atualizando os parâmetros de forma a minimizar a função de custo.
Um exemplo clássico da capacidade das MLPs é a resolução do problema XOR. Como demonstrado anteriormente, esse problema não pode ser resolvido por um perceptron simples devido à sua natureza não linearmente separável. No entanto, ao adicionar uma camada oculta com pelo menos dois neurônios e aplicar funções de ativação não lineares, a MLP é capaz de particionar o espaço de entrada em regiões lineares separáveis, solucionando corretamente o problema.
Método do Gradiente
Para que a rede neural aprenda os pesos que produzem a saída desejada, é necessário calcular a diferença entre a saída prevista pela rede, $\hat{y}$, e a saída correta, $y$, que representa o erro do modelo. Esse erro é então utilizado para ajustar os pesos da rede, de forma que a próxima previsão seja mais próxima do valor esperado. O processo de atualização dos pesos geralmente ocorre por meio do método do gradiente descendente, onde o erro é retropropagado pelas camadas da rede para calcular o impacto de cada peso no resultado final. Assim, os pesos são modificados gradualmente, minimizando a função de custo e melhorando a precisão da rede ao longo do treinamento.
O objetivo do treinamento é minimizar a função custo $E(\mathbf{w})$, que pode ser o erro quadrático médio:
em que $P$ é o número de amostras, $y_k^{(p)}$ é a saída desejada e $\hat{y}_k^{(p)}$ é a saída da rede. Para isso, utiliza-se o gradiente da função custo em relação a cada peso.
Para atualizar os pesos da rede MLP usando o método do gradiente descendente, é necessário calcular o gradiente da função custo em relação a cada peso $w_{ij}^{(l)}$. Esse cálculo é feito usando a regra da cadeia, de acordo com o algoritmo de retropropagação.
Seja $a_j^{(l-1)}$ a ativação do neurônio $j$ na camada anterior $l-1$, $z_i^{(l)} = \sum_k w_{ik}^{(l)} a_k^{(l-1)} + b_i^{(l)}$ a entrada do neurônio $i$ na camada $l$, $a_i^{(l)} = \phi(z_i^{(l)})$ a saída do neurônio $i$ após a função de ativação. Queremos calcular:
Pela regra da cadeia:
Sabemos que:
Definimos o erro local no neurônio $i$ da camada $l$ como:
então o gradiente se torna:
e atualiza-se os pesos pela regra do gradiente descendente:
onde $\eta$ é a taxa de aprendizado.
A figura abaixo ilustra o conceito de descida do gradiente. No gráfico, a curva azul representa a função de erro $E(w)$, que depende do peso $w$. O ponto preto em $w$ mostra o valor atual do peso e o correspondente valor do erro. A seta verde indica o gradiente do erro $\nabla E(w)$ naquele ponto, apontando na direção de maior crescimento da função. Como o objetivo do treinamento é minimizar o erro, a atualização do peso ocorre na direção oposta ao gradiente, indicada pela seta vermelha $-\eta \nabla E(w)$, onde $\eta$ é a taxa de aprendizado. Essa movimentação leva o peso na direção do mínimo da função de erro, mostrado no ponto $w = 1.5$, onde o erro é mínimo e o gradiente é zero.
Implementação da Descida do Gradiente
Abaixo está uma implementação simples em Python do algoritmo de gradiente descendente:
import numpy as np
import matplotlib.pyplot as plt
# Função objetivo
def f(x):
return (x - 3)**2
# Derivada (gradiente)
def grad_f(x):
return 2 * (x - 3)
# Gradiente descendente
x0 = -2 # ponto inicial
eta = 0.1 # taxa de aprendizado
num_iter = 20
# Listas para registrar a trajetória
x_vals = [x0]
f_vals = [f(x0)]
x = x0
for i in range(num_iter):
x = x - eta * grad_f(x)
x_vals.append(x)
f_vals.append(f(x))
# Plot
x_range = np.linspace(-2, 5, 100)
plt.plot(x_range, f(x_range), label='f(x) = (x - 3)^2')
plt.plot(x_vals, f_vals, 'ro--')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradiente Descendente')
plt.legend()
plt.grid(True)
plt.show()Back-propagation
O algoritmo de retropropagação (backpropagation) é um método eficiente para calcular os gradientes em redes neurais multicamadas. Ele usa a regra da cadeia do cálculo diferencial para propagar os erros da camada de saída de volta através da rede.
- Forward Pass: Calcule as saídas de todas as camadas
- Backward Pass: Calcule os gradientes propagando o erro da saída para a entrada
- Atualização: Atualize os pesos usando os gradientes calculados
Para uma rede com $L$ camadas, o algoritmo calcula:
onde $\delta^{(l)}$ representa o erro na camada $l$, $\odot$ denota o produto elemento a elemento, e $\sigma'$ é a derivada da função de ativação.
Funções de ativação
As funções de ativação são componentes cruciais das redes neurais, pois introduzem não linearidades que permitem à rede aprender padrões complexos. Sem funções de ativação não lineares, uma rede neural multicamadas seria equivalente a uma única camada linear.
Função Sigmoide (Logística)
A função sigmoide é uma das funções de ativação mais clássicas, definida por:
Propriedades:
- Saída no intervalo $(0, 1)$
- Diferenciável em todos os pontos
- Monotônica crescente
- Suave e contínua
Derivada:
Função Tangente Hiperbólica
A função tangente hiperbólica é definida por:
Propriedades:
- Saída no intervalo $(-1, 1)$
- Zero-centrada (média das saídas próxima de zero)
- Gradientes maiores que a sigmoide
Derivada:
Função ReLU (Rectified Linear Unit)
A função ReLU é atualmente uma das mais populares, definida por:
Vantagens:
- Computacionalmente eficiente
- Não sofre com gradiente desvanecente para valores positivos
- Promove esparsidade na rede
- Converge mais rapidamente que sigmoide/tanh
Derivada:
Função Softmax
A função softmax é usada principalmente na camada de saída para problemas de classificação multiclasse:
onde $K$ é o número total de classes.
Propriedades:
- Saídas no intervalo $(0, 1)$
- Soma das saídas igual a 1
- Pode ser interpretada como distribuição de probabilidade
- Enfatiza a classe com maior valor de entrada
Métricas de avaliação
A avaliação adequada do desempenho de modelos de redes neurais é fundamental para determinar sua eficácia. As métricas variam dependendo do tipo de problema: classificação ou regressão.
Problemas de classificação
Matriz de Confusão
A matriz de confusão é uma ferramenta fundamental para avaliar modelos de classificação. Para classificação binária, ela é uma matriz 2×2 que compara as predições com os valores reais:
| Real | Predito | |
|---|---|---|
| Positivo | Negativo | |
| Positivo | TP (Verdadeiro Positivo) | FN (Falso Negativo) |
| Negativo | FP (Falso Positivo) | TN (Verdadeiro Negativo) |
Acurácia
A acurácia mede a proporção de predições corretas em relação ao total de predições:
A acurácia é uma métrica intuitiva, mas pode ser enganosa em datasets desbalanceados, onde uma classe é muito mais frequente que a outra.
Precisão
A precisão (ou valor preditivo positivo) mede a proporção de verdadeiros positivos entre todas as predições positivas:
Esta métrica responde à pergunta: "Das instâncias que o modelo classificou como positivas, quantas realmente são positivas?"
Sensibilidade
A sensibilidade (ou recall, ou taxa de verdadeiros positivos) mede a proporção de verdadeiros positivos que foram corretamente identificados:
Esta métrica responde à pergunta: "Das instâncias que realmente são positivas, quantas o modelo conseguiu identificar?"
Problemas de regressão
Para problemas de regressão, onde o objetivo é prever valores contínuos, utilizamos métricas diferentes:
Erro Absoluto Médio (MAE)
Erro Quadrático Médio (MSE)
Raiz do Erro Quadrático Médio (RMSE)
Coeficiente de Determinação (R²)
onde $\bar{y}$ representa a média dos valores reais. Valores de $R^2$ próximos de 1 indicam que o modelo explica bem os dados.
💡 Exercícios de Fixação
Teste seus conhecimentos sobre Redes Neurais Artificiais com estes exercícios interativos. Clique nas respostas para verificar se estão corretas!
Exercício 1: Conceitos Fundamentais
1.1) Qual é a função matemática básica de um neurônio artificial?
1.2) O que representam os pesos ($w_i$) em um neurônio artificial?
Exercício 2: Perceptron
2.1) Por que o perceptron simples não consegue resolver o problema XOR?
2.2) Complete a equação do hiperplano de decisão: $\mathbf{w}^T \mathbf{x} + b = ?$
Exercício 3: Redes Multicamadas
3.1) Qual é a principal vantagem das redes MLP sobre o perceptron simples?
3.2) O algoritmo de backpropagation é usado para:
Exercício 4: Funções de Ativação
4.1) Qual função de ativação tem saída no intervalo (0, 1)?
4.2) Qual é a principal vantagem da função ReLU?
4.3) A função Softmax é usada principalmente em:
Exercício 5: Métricas de Avaliação
5.1) Na matriz de confusão, o que representa um "Falso Positivo"?
5.2) Para problemas de regressão, qual métrica NÃO é apropriada?
🧠 Exercício Prático: Cálculo Manual
Calcule a saída de um neurônio:
Dado um neurônio com:
- Entradas: $x_1 = 0.5$, $x_2 = 0.8$
- Pesos: $w_1 = 1.2$, $w_2 = -0.7$
- Viés: $b = 0.3$
- Função de ativação: ReLU
Passo 1: Calcule $z = w_1x_1 + w_2x_2 + b$
Passo 2: Aplique ReLU: $y = \max(0, z)$
🎓 Parabéns!
Você completou todos os exercícios sobre Redes Neurais Artificiais Feedforward!
📋 Resumo dos Conceitos Aprendidos:
- ✅ Modelo matemático do neurônio artificial
- ✅ Arquitetura e limitações do Perceptron
- ✅ Problema XOR e separabilidade linear
- ✅ Redes Perceptron Multicamadas (MLP)
- ✅ Algoritmo de Backpropagation
- ✅ Funções de ativação (Sigmoide, Tanh, ReLU, Softmax)
- ✅ Métricas de avaliação para classificação e regressão
🏆 Pioneiros das Redes Neurais
O desenvolvimento das redes neurais artificiais é resultado de décadas de pesquisa e contribuições de cientistas visionários. Esta seção homenageia os principais pesquisadores cujas descobertas fundamentaram os conceitos que estudamos neste capítulo.
🧠 Warren McCulloch & Walter Pitts (1943)
Biografia:
Warren McCulloch (1898-1969) foi um neurofisiologista e ciberneticista americano. Walter Pitts (1923-1969) foi um lógico e matemático autodidata que começou a colaborar com McCulloch aos 18 anos.
Contribuição Revolucionária:
Em 1943, publicaram o artigo seminal "A Logical Calculus of Ideas Immanent in Nervous Activity", que estabeleceu o primeiro modelo matemático formal do neurônio artificial. Eles demonstraram que neurônios artificiais simples poderiam realizar qualquer função lógica.
Modelo Proposto:
$$y = \phi\left(\sum_{i=1}^{n} w_i x_i + b\right)$$
Esta equação fundamental ainda é a base de todos os neurônios artificiais modernos!
Impacto:
- Criaram os fundamentos matemáticos para a inteligência artificial
- Estabeleceram a conexão entre lógica e neurobiologia
- Influenciaram John von Neumann no desenvolvimento da arquitetura de computadores
⚡ Frank Rosenblatt (1958)
Biografia:
Frank Rosenblatt (1928-1971) foi um psicólogo americano e pioneiro da inteligência artificial. Trabalhou no Cornell Aeronautical Laboratory e mais tarde tornou-se professor em Cornell.
O Perceptron:
Em 1958, Rosenblatt desenvolveu o Perceptron, a primeira rede neural artificial capaz de aprender. Ele construiu uma máquina física chamada "Mark I Perceptron" que podia reconhecer padrões visuais simples.
Regra de Aprendizado do Perceptron:
$$w_i = w_i + \eta (y - \hat{y}) x_i$$
Primeira regra de aprendizado automático para ajustar pesos!
Legado:
- Demonstrou que máquinas podem aprender por experiência
- Inspirou a primeira onda de interesse em redes neurais (1950s-1960s)
- O algoritmo do perceptron ainda é usado hoje em machine learning
Curiosidade histórica: Rosenblatt foi otimista demais sobre as capacidades do perceptron, prevendo que ele logo seria capaz de "reconhecer pessoas, chamar seu nome e traduzir idiomas".
❄️ Marvin Minsky & Seymour Papert (1969)
Biografia:
Marvin Minsky (1927-2016) e Seymour Papert (1928-2016) foram pioneiros da IA no MIT. Minsky fundou o laboratório de IA do MIT e Papert desenvolveu a linguagem de programação Logo.
Análise Crítica:
Em 1969, publicaram "Perceptrons", um livro que demonstrou matematicamente as limitações fundamentais do perceptron simples, incluindo sua incapacidade de resolver o problema XOR.
Problema XOR Demonstrado:
Provaram que não existem pesos $w_1, w_2, b$ tais que:
$$w_1 \cdot 0 + w_2 \cdot 0 + b < 0$$ $$w_1 \cdot 0 + w_2 \cdot 1 + b \geq 0$$
$$w_1 \cdot 1 + w_2 \cdot 0 + b \geq 0$$ $$w_1 \cdot 1 + w_2 \cdot 1 + b < 0$$
Consequências:
- Causaram o primeiro "inverno da IA" (1970s-1980s)
- Reduziram drasticamente o financiamento para pesquisa em redes neurais
- Paradoxalmente, motivaram o desenvolvimento de redes multicamadas
Ironia histórica: Embora tenham "enterrado" temporariamente as redes neurais, suas críticas foram essenciais para o desenvolvimento posterior das MLPs que resolveram exatamente os problemas que eles identificaram.
🚀 David Rumelhart, Geoffrey Hinton & Ronald Williams (1986)
Biografia:
David Rumelhart (1942-2011) foi psicólogo cognitivo em Stanford. Geoffrey Hinton (1947-) é considerado um dos "pais do deep learning" e Prêmio Turing 2018. Ronald Williams (1946-) é cientista da computação especialista em aprendizado por reforço.
O Algoritmo Revolucionário:
Em 1986, publicaram "Learning representations by back-propagating errors", apresentando o algoritmo de backpropagation que tornou possível treinar redes neurais profundas eficientemente.
Backpropagation:
Forward pass: $$a^{(l)} = \phi(W^{(l)} a^{(l-1)} + b^{(l)})$$
Backward pass: $$\delta^{(l)} = ((W^{(l+1)})^T \delta^{(l+1)}) \odot \phi'(z^{(l)})$$
Atualização: $$W^{(l)} := W^{(l)} - \eta \delta^{(l+1)} (a^{(l)})^T$$
Revolução Científica:
- Ressuscitaram o campo das redes neurais
- Tornaram possível treinar redes com múltiplas camadas ocultas
- Estabeleceram as bases para o deep learning moderno
- Permitiram resolver o problema XOR e muitos outros
Curiosidade: Geoffrey Hinton hoje trabalha no Google e é considerado o "padrinho do deep learning", tendo orientado muitos dos líderes atuais da área como Yann LeCun e Yoshua Bengio.
🧲 John Hopfield (1982)
Biografia:
John Hopfield (1933-) é um físico americano que aplicou conceitos da física estatística às redes neurais, criando uma ponte fundamental entre física e neurociência computacional.
Contribuição:
Introduziu as Redes de Hopfield em 1982, demonstrando como redes neurais podem funcionar como memórias associativas usando princípios da mecânica estatística.
Função de Energia de Hopfield:
$$E = -\frac{1}{2} \sum_{i,j} w_{ij} s_i s_j$$
A rede converge para mínimos locais desta função energia!
Legado:
- Trouxe rigor matemático da física para redes neurais
- Inspirou pesquisas em otimização neural
- Influenciou o desenvolvimento de máquinas de Boltzmann
📅 Linha do Tempo das Redes Neurais
McCulloch & Pitts
Primeiro modelo matemático do neurônio artificial
Rosenblatt
Perceptron - primeira rede neural que aprende
Minsky & Papert
Limitações do perceptron - início do "inverno da IA"
Hopfield
Redes de Hopfield - física encontra neurociência
Rumelhart, Hinton & Williams
Backpropagation - renascimento das redes neurais
Era do Deep Learning
CNNs, RNNs, Transformers - revolução da IA moderna
💭 Reflexão
O desenvolvimento das redes neurais artificiais ilustra perfeitamente como a ciência progride: através de colaboração, crítica construtiva, e perseverança diante de obstáculos. Cada "fracasso" (como as limitações do perceptron) levou a avanços ainda maiores (como as redes multicamadas).
Hoje, quando usamos ChatGPT, reconhecimento de imagens, ou tradução automática, estamos utilizando descendentes diretos das ideias pioneiras destes cientistas visionários que ousaram modelar matematicamente o funcionamento do cérebro humano.
"Se vi mais longe, foi por estar sobre ombros de gigantes."